Viquiprojecte:CEPA Sa Pobla/ESPA/Matemàtiques/Matemàtiques 2.2/Unitat 2. Funcions/Tipus de funcions

Funcions afins

L'expressió algebraica d'una funció afí és

$f(x)=mx+n$

o també

$y=mx+n$

on $m,n$ són dos nombres reals.

Les funcions afins es representen gràficament com rectes.

El valor $m$ indica la inclinació d'aquesta recta i per això s'anomena pendent

El valor $n$ indica l'altura sobre l'eix OY per on passa la recta i per això s'anomena ordenada a l'origen

Casos particulars

Si $m=0$ aleshores l'expressió algebraica és $f(x)=n$ i s'anomena funció constant. La seva representació gràfica correspon a una recta horitzontal.

Si $n=0$ aleshores l'expressió algebraica és $f(x)=mx$ i s'anomena funció de proporcionalitat. La seva representació gràfica correspon a una recta que passa per l'origen.

Representació gràfica

• 
  Funcions constats
• 
  Funció de proporcionalitat
• 
  Funcions afins

Aplicacions

Càlcul de tarifes en què hi ha una quota fixa i una part que depèn de la quantitat adquirida o consumida. Per exemple:

• Cost d'una telefonada, amb un cost fix per començar la telefonada i una part que depèn de forma proporcional al temps transcorregut durant la telefonada.
• Cost de la factura elèctrica, amb un cost fix per a la potència contractada i una part que depèn de forma proporcional a l'energia consumida.
• Cost del combustible repostat que depèn de forma proporcional als litres introduïts al depòsit.
• Cost d'una tarifa planes d'internet, de telèfon, etc.

Funcions quadràtiques

Són funcions que tenen expressió algebraica

$f(x)=a{x}^2+bx+c$

on $a,b,c$ són nombres reals i a més $a\ne 0$

La seva representació gràfica és una paràbola amb el seu eix de simetria de forma vertical.

Representació gràfica

• 
  Funció quadràtica $f(x)=x^2-x-2$

Aplicacions

Qualsevol fenomen físic que depengui de la gravetat. Per exemple:

• Tir parabòlic. Càlcul de distàncies i altures.
• Caiguda lliure. Càlcul del temps de caiguda o de l'altura.
• Llançament d'objectes enlaire. Càlcul de l'altura màxima, el temps necessari, etc.

Estudi de fenòmens relacionats amb la conducció de vehicles.

• El drag o resistència de l'aire depenent de la velocitat.
• La força centrífuga quan es fa un gir.
• La distància de frenada i la distància de detenció.

Funcions radicals

Són funcions de la forma

$f(x)=\pm \sqrt{ax+b}$

on $a,b$ són nombres reals.

Representació gràfica

La seva representació gràfica correspon a mitja paràbola amb el seu eix de simetria situat horitzontalment.

• 
  Paràbola tombada. Només es pot considerar funció radical la meitat superior o la meitat inferior.

Aplicacions

Aquelles en què intervengui una funció quadràtica i s'hagi de calcular alguna dada en sentit invers al de la funció quadràtica.

Funcions exponencials

Són funcions de la forma

$f(x)=a^x$

on $a$ és un nombre real positiu i que a més ha de ser diferent de 1.

Representació gràfica

La seva representació gràfica és una corba que mostra una tendència a un costat i un creixement exagerat a l'altre costat.

• 
  Diverses funcions exponencials:

  • Vermella: $f(x)=e^x$
  • Verda: $g(x)=10^x$
  • Blava: $h(x)=1.7^x$

Com més gran és el nombre $a$, més ràpidament creix la corba.

Si el nombre $a$ és menor que 1, la corba és decreixent.

Aplicacions

Estudi de fenòmens biològics. Per exemple:

• Creixement d'una colònia de bacteris. Estimació del nombre d'individus passat un temps determinat.
• Propagació d'una epidèmia en funció de la $R_0$. Estudi de corbes que es descontrolen i presa de mesures per pal·liar els efectes.

Funcions logarítmiques

Són funcions de la forma

$f(x)={\log }_{b}x$

on $b$ és un nombre real positiu i diferent de 1.

El logaritme és l'operació definida com el nombre $L$ que compleix l'equació següent:

$b^L=x$

Exemples

Fixa't en aquestes dues taules:

Casos particulars

La funció del logaritme decimal és $f(x)=\log x$. S'entén que la base és el nombre 10.

La funció del logaritme neperià és $f(x)=\ln x$. S'entén que la base del logaritme és el nombre $e$

Representació gràfica

• 
  Funcions logarítmiques

Aplicacions

Totes aquelles en què hi hagi involucrada una funció exponencial. Per exemple:

• Creixement de colònies de bacteris. Calcular el temps necessari per arribar a una certa població.
• Control d'una epidèmia depenent de la $R_0$. Estimació del temps en què s'arribarà a la saturació dels serveis sanitaris i presa de decisions.
• Comparació de nombres molt grans i molt petits. El logaritme decimal permet comparar ordres de magnitud.

Funció de proporcionalitat inversa

Són funcions amb expressió algebraica

$f(x)=\frac{a}{x-b}+c$

on $a,b,c$ són nombres reals i $a\ne 0$

Representació gràfica

• 
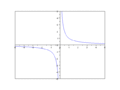
  Funció de proporcionalitat inversa

Aplicacions

Aquelles en què intervenguin dues variables que actuen una al revés de l'altra, de forma que quan una augmenta l'altra ha de disminuir. Per exemple:

• Nombre de persones realitzant una tasca i temps necessari per completar-la.

Funcions trigonomètriques

Són funcions en què les variables són angles, mesurats en graus o en radians i el resultat és una proporció de longituds.

Hi ha un conjunt extens de funcions que es consideren trigonomètriques. Són funcions periòdiques, ja que els angles es van repetint cada 360º o, equivalentment, cada $2\pi$ radians.

Casos particulars

La funció sinus $f(x)=\sin x$

La funció cosinus $f(x)=\cos x$

La funció tangent $f(x)=\tan x$

Representació gràfica

• 
  Funcions trigonomètriques

Aplicacions

Qualsevol càlcul en què intervengui un triangle. Per exemple:

• Càlcul d'altures
• Càlcul de distàncies
• Càlcul d'angles

Funcions definides a trossos

Són funcions amb una expressió algebraica escrita com una llista d'alternatives i condicions.

$f(x)=\{\begin{array}{cc}{g}_1(x)& \text{ si condició 1 sobre }x\\ g_2(x)& \text{ si condició 2 sobre }x\\ \dots \end{array}$

Exemple

La funció valor absolut, que retorna el mateix nombre amb el signe convertit a positiu.

$Vabs(x)=\{\begin{array}{cc}x& \text{ si }x\ge 0\\ -x& \text{ si }x<0\end{array}$

Representació gràfica

Sol ser un gràfic amb trams juxtaposats, com si haguessin enganxat retalls d'altres gràfiques, una devora l'altra.

• 
  Funció valor absolut
• 
  Funció definida per dos trossos quadràtics
• 
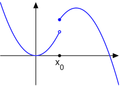
  Funció definida per trams rectes
• 
  Funció part entera

Exercici

Elaborau un quadre resum de totes les funcions vistes anteriorment:

Tipus de funció	Expressió algebraica	Representació gràfica	Algunes aplicacions i propietats
Funció constant
Funció de proporcionalitat
Funció afí
Funció quadràtica
Funció radical
Funció exponencial
Funció logarítmica
Funció de proporcionalitat inversa
Funcions trigonomètriques