Cinemàtica/Models cinemàtics

A continuació hi ha un recull dels models de moviment més habitualment utilitzats.

Moviments rectilinis

Un moviment rectilini és aquell moviment on el cos que es mou té una trajectòria rectilínia.

Moviment rectilini uniforme

És aquell moviment rectilini que es produeix quan el cos es mou amb velocitat constant.

Es formula de la següent manera:

$𝐱={𝐱}_{\mathrm{𝟎}}+𝐯\cdot 𝐭$

$𝐯=constant$

$𝐚=0$

Moviment rectilini uniformement accelerat

Es aquell moviment rectilini on la velocitat varia constantment, o sigui, existeix una acceleració constant diferent de 0.

Les fórmules bàsiques són:

$𝐱={𝐱}_{\mathrm{𝟎}}+{𝐯}_{\mathrm{𝟎}}\cdot 𝐭+\frac{𝐚\cdot {𝐭}^{\mathrm{𝟐}}}{2}$

$𝐯={𝐯}_{\mathrm{𝟎}}+𝐚\cdot 𝐭$

$𝐚=constant$

A més, resulta molt útil aquesta:

${{𝐯}_{𝐟}}^2-{{𝐯}_{𝐨}}^2=2\cdot 𝐚\cdot \mathrm{\Delta }{𝐱}^2$

Cas particular de la caiguda lliure

Es considera caiguda lliure al model de moviment on un cos cau a causa de l'acció de la gravetat. L'acceleració en aquest cas és l'acceleració de la gravetat, en la superfície de la Terra g=-9.81 m/s². No es té en compte la fricció de l'aire ni les variacions que sofreix la gravetat en la superfície de la Terra. S'acostuma a agafar com a sistema de referència aquell que consisteix en una línia vertical on cap amunt es considera positiu, i cap avall negatiu. D'aquesta manera un cos que baixa té un desplaçament negatiu, i un que puja té un desplaçament positiu. En aquest sistema és important agafar l'acceleració amb valor negatiu.

Si prenem h com alçada, les fórmules resulten:

$𝐡={𝐡}_{\mathrm{𝟎}}+{𝐯}_{\mathrm{𝟎}}\cdot 𝐭+\frac{𝐠\cdot {𝐭}^{\mathrm{𝟐}}}{2}$

$𝐯={𝐯}_{\mathrm{𝟎}}+𝐠\cdot 𝐭$

$𝐠=-9.81{\text{ m/s}}^2$

${{𝐯}_{𝐟}}^2-{{𝐯}_{𝐨}}^2=2\cdot 𝐠\cdot \mathrm{\Delta }{𝐡}^2$

A cinemàtica, s'anomena moviment harmònic a aquell moviment on un cos passa periòdicament pels mateixos punts de la seva trajectòria.

Moviment harmònic simple

Relació entre el moviment circular i el moviment harmònic

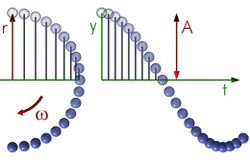
Quan el període d'un moviment harmònic es constant, s'anomena moviment harmònic simple.

La seva formulació és la següent:

$𝐱={𝐱}_0+𝐀\cdot \sin ({\varphi }_0+\omega \cdot 𝐭)$

$𝐯=𝐀\cdot \omega \cdot \cos ({\varphi }_0+\omega \cdot 𝐭)$

$𝐚=-𝐀\cdot {\omega }^2\cdot \sin ({\varphi }_0+\omega \cdot 𝐭)$

On $𝐀$ és l'amplada de l'oscil·lació.

Es defineix com freqüència, $𝐟$, el nombre d'oscil·lacions que fa el cos en un temps determinat. El període, $𝐓$, és l'invers de la freqüència, i es defineix com el temps que triga el cos en fer una oscil·lació.

$𝐓=\frac{1}{𝐟}$

Existeix una correspondència entre el moviment circular i el moviment harmònic simple. Si formulem un moviment circular uniforme en coodenades rectangulars, el resultat és el següent:

$𝐱=𝐫\cdot \cos ({\varphi }_0+\omega \cdot 𝐭)$

$𝐲=𝐫\cdot \sin ({\varphi }_0+\omega \cdot 𝐭)$

Les dues coordenades mirades separadament, es corresponen a un moviment harmònic simple. De la mateixa manera es pot considerar qualsevol moviment harmònic simple generat per un moviment circular uniforme, del qual només es té en compte una coordenada. La velocitat angular, $\omega$, i l'angle inicial,${\varphi }_0$, corresponen a aquest hipotètic moviment circular.

Moviments en el pla

Moviment circular

Esquema d'un moviment circular

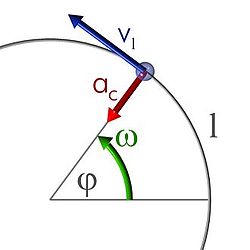
Un moviment circular es un model de moviment en el pla, on el cos que es mou té una trajectòria circular.

Moviment circular uniforme

Moviment on el cos que es mou té trajectoria circular i porta una velocitat angular constant.

La formulació d'aquest moviment es dóna en coordenades polars. Donat un angle inicial ${\varphi }_0$ i una velocitat angular $\omega$:

$\varphi ={\varphi }_0+\omega \cdot 𝐭$

Relacionats amb la velocitat angular, s'acostumen a emprar dos conceptes en aquest model:

• Freqüència, $𝐟$, definida com la quantitat de voltes que es fan en un temps determinat.

$𝐟=\frac{\omega }{2\cdot \pi }$

• Període, $𝐓$, definit com el temps que triga el cos en fer una volta sencera.

$𝐓=\frac{1}{𝐟}$

Les magnituds angulars es relacionen amb les magnituds lineals tal com segueix:

• La longitud, $𝐥$ , d'un arc determinat per un angle $\varphi$, ve donada per:

$𝐥=\varphi \cdot 𝐫$

• La velocitat lineal d'un cos en moviment circular ve donada per:

${𝐯}_{𝐥}=\omega \cdot 𝐫$

• La distància recorreguda per un cos en moviment circular és:

$d=\omega \cdot 𝐭\mathbf{\cdot }𝐫$

• En tot moviment circular apareix una acceleració centrípeta que va variant la direcció del cos en moviment.

${𝐚}_{𝐜}={\omega }^2\cdot 𝐫$

L'acceleració centrípeta es perpendicular al vector velocitat, apuntant cap al centre de la trajectòria circular.

Tir parabòlic

Esquema d'un tir parabòlic.

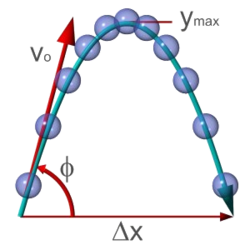
El tir parabòlic és un model de moviment, que estudia com es mou un cos llançat sota els efectes de la gravetat. El cos descriu llavors una trajectòria parabòlica.

En aquest model s'utilitza un sistema de referència on l'eix x és horitzontal i l'eix y és vertical. L'origen del sistema se situa en el punt de llançament. S'utilitzen coordenades rectangulars.

El moviment es modelitza com la composició de dos moviments rectilinis, un per cada coordenada. La coordenada x només es mou per l'acció de la velocitat inicial i per tant serà un moviment rectilini uniforme. La coordenada y sofreix l'acció de la gravetat i és un moviment rectilini uniformement accelerat.

Es considera que el cos es llança a una velocitat inicial ${𝐯}_{\mathrm{𝟎}}$ i amb un angle $\varphi$ concret. Les velocitats del cos en les components x i y es troben com segueix:

${𝐯}_{\mathrm{𝟎}𝐱}={𝐯}_{\mathrm{𝟎}}\cdot cos\varphi$

${𝐯}_{\mathrm{𝟎}𝐲}={𝐯}_{\mathrm{𝟎}}\cdot sin\varphi$

Les components ${𝐯}_{\mathrm{𝟎}𝐱}$ i ${𝐯}_{\mathrm{𝟎}𝐲}$, compleixen la propietat:

${{𝐯}_{\mathrm{𝟎}}}^2={{𝐯}_{\mathrm{𝟎}𝐱}}^2+{{𝐯}_{\mathrm{𝟎}𝐲}}^2$

La posició del cos en moviment es troba amb les dues expressions:

$𝐱={𝐯}_{\mathrm{𝟎}𝐱}\cdot 𝐭$

$𝐲={𝐯}_{\mathrm{𝟎}𝐲}\cdot 𝐭-\frac{𝐠{𝐭}^2}{2}$

S'agafa el valor absolut de l'acceleració de la gravetat,$𝐠=9.8m/s^2$,per simplificar.

Amb aquestes dues expressions podem trobar l'equació de la trajectòria:

$𝐲=\frac{{𝐯}_{\mathrm{𝟎}𝐲}}{{𝐯}_{\mathrm{𝟎}𝐱}}\cdot 𝐱-\frac{𝐠}{2{{𝐯}_{\mathrm{𝟎}}𝐱}^2}\cdot {𝐱}^2$

Dues dades que es calculen habitualment en tir parabòlic són l'abast i l'altura màxima.

L'abast és la distància horitzontal recorreguda pel cos quan torna a tenir alçada 0. Per calcular-ho es substitueix per 0 la y a l'equació de trajectòria:

$0=\frac{{𝐯}_{\mathrm{𝟎}𝐲}}{{𝐯}_{\mathrm{𝟎}𝐱}}\cdot 𝐱-\frac{𝐠}{2{{𝐯}_{\mathrm{𝟎}}𝐱}^2}\cdot {𝐱}^2$

D'on s'extreu que $\mathrm{\Delta }𝐱$ pot ser 0 (punt de sortida) o ser:

$\mathrm{\Delta }𝐱=\frac{{𝐯}_{\mathrm{𝟎}𝐱}\cdot {𝐯}_{\mathrm{𝟎}𝐲}}{𝐠}$

Aquest valor correspon a l'abast.

L'alçada màxima és el màxim valor que agafa la coordenada y. Quan el cos arriba a l'alçada màxima la velocitat vertical és nul·la. La velocitat vertical segueix la següent expressió:

${𝐯}_{𝐲}={𝐯}_{\mathrm{𝟎}𝐲}-𝐠\cdot 𝐭$

Si substituim ${𝐯}_{𝐲}$ per 0 i aillem $𝐭$

$𝐭=\frac{{𝐯}_{\mathrm{𝟎}𝐲}}{𝐠}$

Substituint t a l'equació de l'alçada i simplificant, s'arriba a que l'alçada màxima és:

${𝐲}_{𝐦𝐚𝐱}=\frac{{{𝐯}_{\mathrm{𝟎}𝐲}}^2}{2𝐠}$